Beloved of high school students, algebra is the part of maths where letters or symbols are used to stand for numbers. It helps us solve problems and figure out things when we don’t know all the numbers yet. For example, if we know part of a puzzle, algebra helps us find the missing piece. It’s like solving a maths mystery!
Learners use algebra, perhaps without realising it. For example, when subtracting, a form of algebra is utilised. The question 8 – 5 can be rephrased to ask instead, “What is added to 5 to make 8?” This is algebraic rearrangement by another name.
The same is true for a division question such as 12 ÷ 4. Learners often struggle with division questions when they have no problem with the corresponding multiplication fact. Asking instead, “What number is multiplied by 4 to give 12?” prompts learners to use their knowledge of the 4 times table to answer the question.
Use simple formulae
The most obvious use of formulae for learners is with area and perimeter calculations. For example, for a rectangle, the area is calculated by multiplying the length by the width. Since the actual values for these dimensions will vary from rectangle to rectangle, it is easier to remember the general, algebraic formula.
As can be seen, there is also an algebraic formula for calculating the perimeter of a rectangle. A note of caution must be introduced here. Learners need to understand what area and perimeter represent to use these formulas.
The memorisation of formulas is a subject for debate. On the one hand, the knowledge of how to calculate the area of a rectangle is important. However, formulas will soon be forgotten without a thorough grasp of the underlying principles, leaving learners back at square one.
Algebra is an excellent way to promote this understanding, bringing the argument full circle. Remember that, for any rectangle, the area is calculated by multiplying the length by the width.
Generate and describe linear number sequences
At first, learners should be taught how to recognise and describe linear number sequences. They should describe the rule using words rather than algebraic notation. Once this has been understood, learners should move on to using algebraic notation to write the formula for the nth term. This is a
A linear sequence is one where the gap between each term is the same. In later maths, learners encounter quadratic sequences. With these, rather than the terms themselves, the gap between each term will increase or decrease by the same amount.
Express missing number problems algebraically
Using contexts with which they are familiar, learners will use symbols and letters to represent variables and unknowns. For example, when given a triangle with 2 angles given. In this instance, prior knowledge of triangles is used – i.e., all the angles add up to 180°.
If read out loud, a problem might be, “What is the third, unknown angle in a triangle when the other two are 63 degrees and 42 degrees?”
From this, if we call the unknown angle 
, an equation can be written and solved:
Find pairs of numbers that satisfy an equation with two unknowns
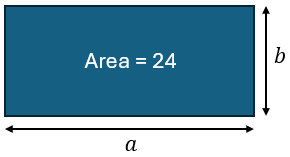
In this instance, a few solutions exist to a given problem. For example, learners might be asked to find possible pairs of values such that 
.
Diving into the question, we see that we need to calculate the pairs of values that multiply together to make 24. A systematic approach is required, but there is no algebraic solution to a single equation with two unknowns. Using the letters 
and 
helps us see how best to find the possible values. If need be, a diagram could be generated to lend further assistance.
Enumerate the possibilities of combinations of two variables
Following the previous example, problems are posed with a single equation, but two unknowns. However, guidance is given. It may be that a range of values for either or both unknowns is given, or values for one of the unknowns are given and learners must calculate the other.
So, there we are. Algebra is a great tool for investigating problems where we don’t have all the necessary information. Instead, we use letters to represent or stand in for them. Potentially, this makes algebra more abstract than arithmetic and therefore, the problems that learners have with it are not surprising.
However, if the idea of something even more abstract than numbers can be overcome, Algebra can help by teaching structured and systematic approaches to problem-solving. Learners sometimes get overwhelmed with more difficult problems. Algebra enables individuals to break down complex issues into smaller, manageable parts.
Furthermore, algebra requires logical and critical thinking. This encourages learners to analyse situations and identify patterns. It also assists with logical reasoning, which is crucial for understanding and applying concepts across various disciplines.