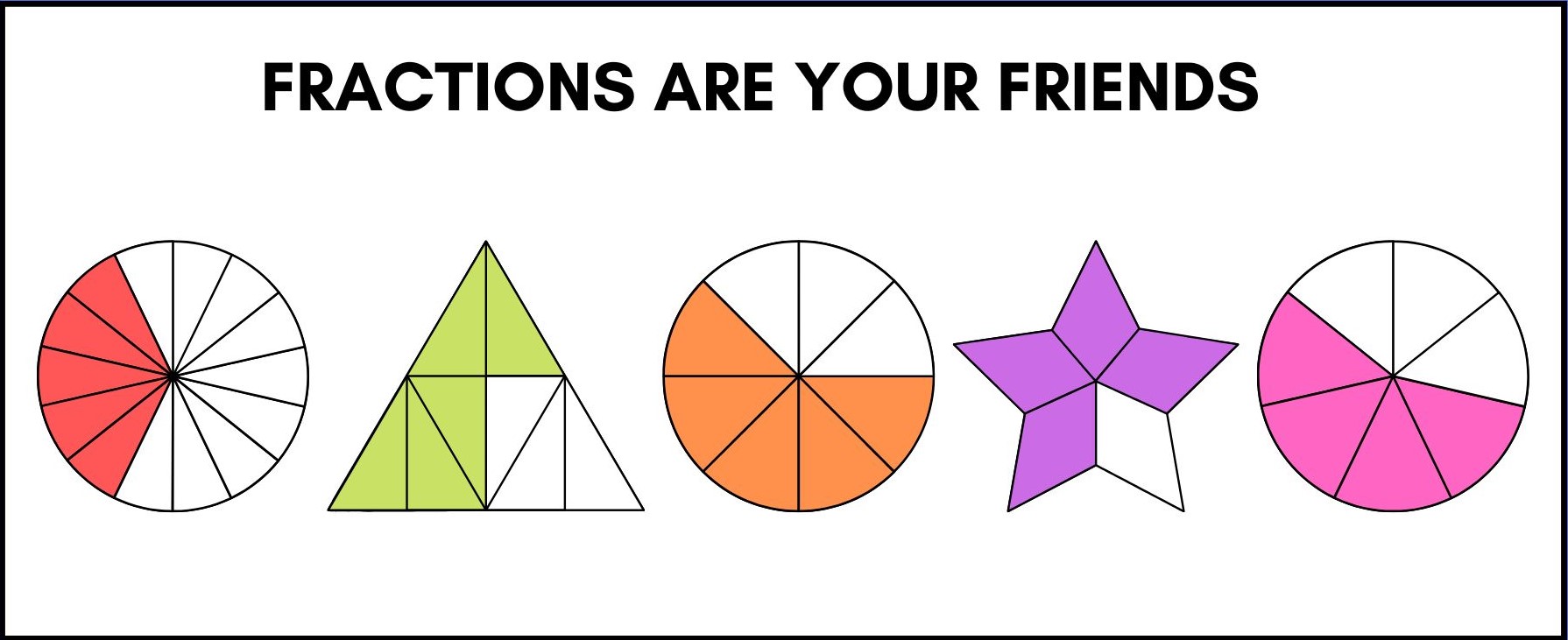
Fractions, Decimals And Percentages

A fraction is a numerical quantity that is a part, or a number of parts, of an object, shape or quantity.

It is best to start off with simple fractions such as halves and quarters. Take a delicious pizza. If you make a single cut, straight down the middle, you end up with two equally sized pieces. These are halves.

Repeat the process, cut both halves in two and we now have four quarters.

So, our pizza has been cut it in half and those two halves were also cut in half. What was one whole was then two halves and finally four quarters.

Don’t be shy about using everyday items to help reinforce their meaning. Pizzas are great, but don’t rely only on them. Vary the shapes used, e.g. use chocolate bars. Initially, don’t use numbers of items – stick to the idea of equal parts. The idea of equal groups moves us towards calculating with fractions.

There is plenty of time for that later. What is important initially is for learners to be comfortable with the idea of fractions as equal parts of objects or shapes. Having a good visual understanding of fractions is vital.

Manipulating physical representations can significantly boost learners’ confidence and understanding, paving the way for more complex fraction concepts later.

Once learners have got a handle on the basics of halves and quarters, it’s time to dive into the wider world of fractions. They are more than just slices of pizza; they are seriously useful numbers that can help us make sense of many situations.

How Do We Write Fractions?

At this point, it is useful to begin to use the correct notation for fractions.

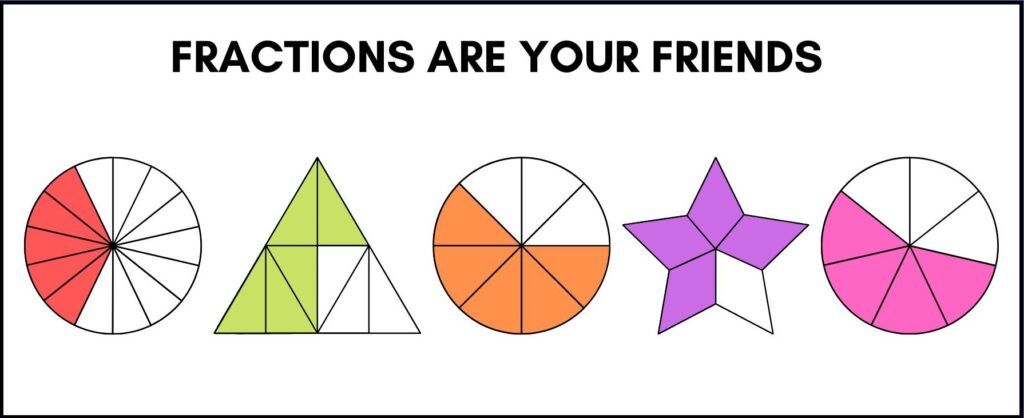
There are three parts to a traditional or ‘vulgar’ fraction. Two numbers and a line.

We call the bottom number the denominator. It tells us how many equal parts the whole has been divided into. We call the top number the numerator. This tells us how many of those equal parts are being considered.

The line in between is known as the vinculum. When we calculate with fractions it is used to show that we divide the numerator by the denominator. We do not need to worry about it at this stage.

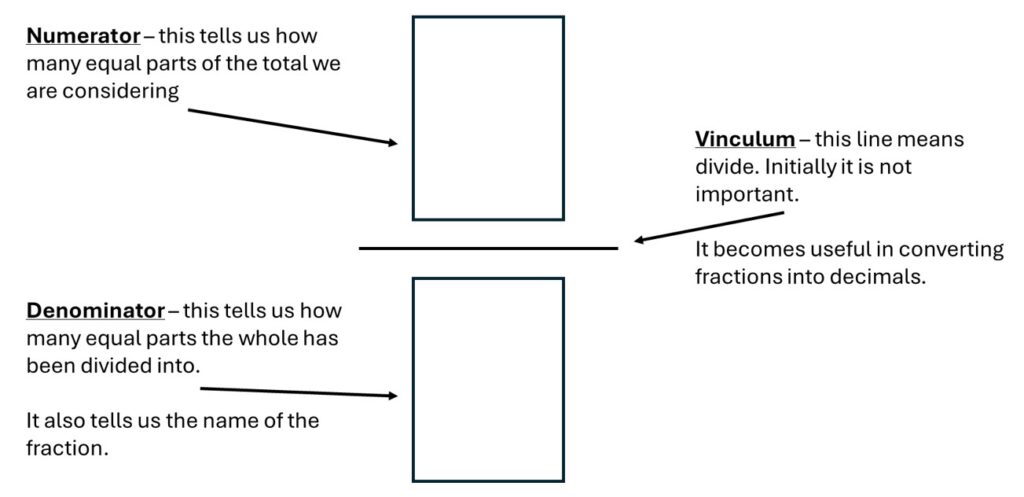
The simplest fractions are unit fractions. These are fractions where the numerator is one. We are considering just one part out of the total number of equal parts. So, one half or one quarter, one third, one sixth, one twelfth and so on.

As we have seen with halves and quarters, unit fractions are the simplest ones. For example, a third is one part when you divide something equally into three. Non-unit fractions are when you have more than one piece of the whole, like two-thirds, where you’re talking about two out of those three parts.

Fractions are read from top to bottom, but they are defined from bottom to top. For example, if we have three-eighths, written out this is $\frac{3}{8}$ . The whole has been divided into a total of 8 equal parts, and we are considering 3 of them.

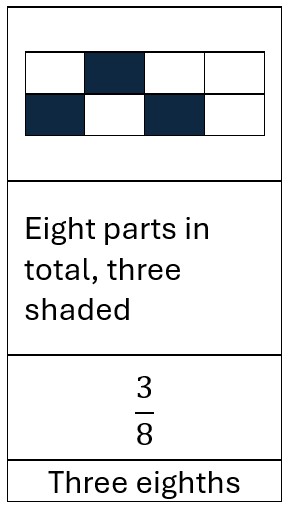
The distinction between denominator and numerator is crucial yet confusing. To help overcome this confusion, I would refer back to the definition of the various parts of a fraction, with a representation to illustrate.

The bottom number (the denominator) tells us how many equal parts the whole has been divided into. The top number (the numerator) tells us how many of those parts we are considering.

Mastering Equivalent Fractions and Simplification

Once you’re comfortable with the basics of fractions, it’s time to look at equivalent fractions. These might seem tricky at first, but they’re just different ways of expressing the same value. Fractions hide in plain sight.

Of course, it is useful to see this visually:

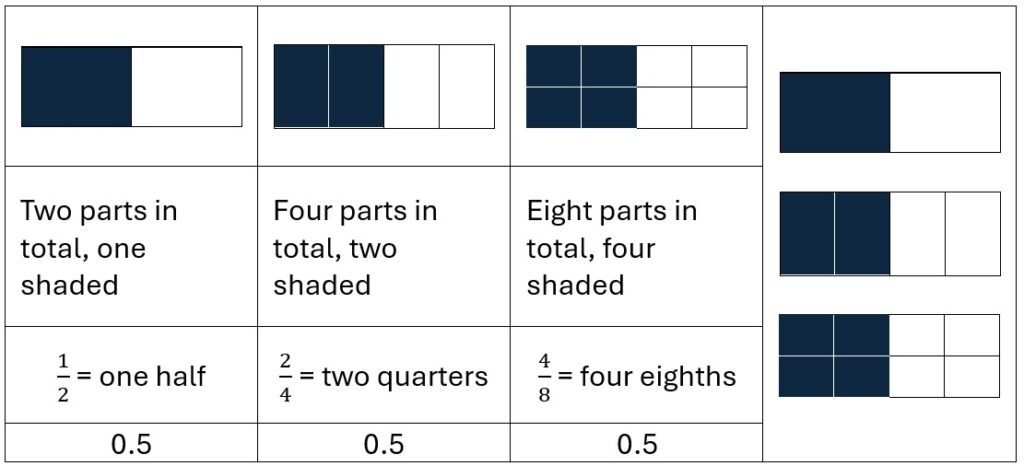
And this is the first time the vinculum plays a part as a dividing line. Divide the numerator by the denominator reveals the fraction’s value as a decimal. If two fractions are equivalent, they have the same decimal value.

A deeper understanding of equivalent fractions

Moving forward, it is important that learners can calculate equivalent fractions. It’s not just about being able to recognise pictorial or concrete representations.

A key skill in being able to calculate equivalent fractions is times table knowledge.

All fractions can be written as equivalent fractions. This is done by multiplying both the numerator and the denominator by the same amount. We end up with an equivalent fraction that has bigger numerator and denominator than the original fraction.

It is a little trickier to convert fractions into equivalent fractions with a smaller numerator and denominator. It is also not always possible.

The first requirement is to be able to spot a fraction that can be written as an equivalent fraction with smaller numerator and denominator. Times tables knowledge is crucial.

If both the numerator and denominator of a fraction appear in the same times table, then it is possible to convert to an equivalent fraction. Once this has been spotted, both numerator and denominator need to be divided by the number whose table they appear in.

For example, $\frac{8}{24}$ can be converted into equivalent fractions with a smaller numerator and denominator than 8 and 24:

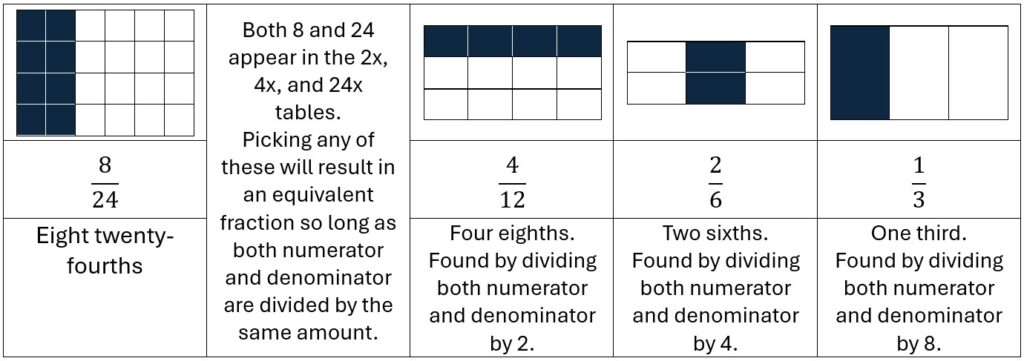
All these fractions here are equivalent to $\frac{8}{24}$ . At this stage, we are trying to encourage learners to focus more on the numbers than match shapes. Hence the representations provided here, whilst accurate, are not all oriented the same way and have different thirds shaded.

What we are saying is that $\frac{8}{24}$ = $\frac{4}{12}$ = $\frac{2}{6}$ = $\frac{1}{3}$

If you punch the fractions into a calculator, e.g. 8 ÷ 24, they all give the same decimal value, i.e. 0.33333333… – after all they are equivalent, so they must have the same value.

Being able to convert fractions into suitable equivalents is a handy skill to have up your sleeve. Fractions cannot be added or subtracted if they do not have the same denominator.

Writing A Fraction In Its Simplest Form

Another, more specific form of an equivalent fraction is expressing a fraction in its simplest form. Writing a fraction with as small a numerator and denominator as possible. The way to do this is to find the highest common factor (HCF) for the numerator and denominator.

For example, if you have $\frac{7}{35}$ , you can divide both the numerator and the denominator by 7 to get $\frac{1}{5}$ . I am sure you will agree, it’s much cleaner, right?

Staying sharp with equivalent fractions and simplification helps to make more complex maths more approachable. It might seem tedious at first, but the practice pays off in your ability to solve problems more efficiently.

Linking Fractions to Decimals

After mastering equivalent fractions and simplification, linking fractions to decimals is the next step. This connection is important because decimals are often used in measurement, money, and data.

Starting with simple fractions like $\frac{1}{2}$ or $\frac{1}{4}$ helps. If you think about money, you need to 50 pence pieces to make a pound. So, 50p is half a pound. Written as a decimal, we find that 50p or half a pound is £0.50.

Similarly, $\frac{1}{4}$ of a pound is £0.25. If there were a 25p coin, you would need 4 to make a pound. These conversions make decimals feel more intuitive, as they’re directly connected to real-life values.

There are some fractions, that ideally need to be memorised. However, if memory fails, we can come back to the idea of a fraction representing the division of the numerator by the denominator.

So, going back to $\frac{1}{2}$ , we can see that a half is 1 divided by 2. Using bus stop method:

For a quarter, the process is pretty much the same, only we divide 1 by 4:

Facing fractions and decimals together may seem daunting. For example, how on Earth are the 1 and 2 of a half linked to the 5 of 0.5? Hopefully, the first example, above, shows this. This method works for converting all fractions into decimals.

As with all Maths ideas, starting small and keeping on practising is key. By linking the two ideas of fractions and decimals, you develop a flexible understanding that helps untangle numerical problems efficiently, whether in the classroom or in practical, day-to-day contexts.

Exploring Mixed Numbers and Improper Fractions

After understanding how fractions relate to decimals, let’s tackle mixed numbers and improper fractions. These are just two different ways to express numbers greater than one.

A mixed number combines a whole number with a fraction, like $3\frac{1}{2}$ . This indicates three wholes and a half. Alternatively, improper fractions have numerators larger than their denominators. So, $3\frac{1}{2}$ would be written as $\frac{7}{2}$ as an improper fraction.

Converting between the two is a key skill. First, let’s turn a mixed number into an improper fraction.

How do we know that $3\frac{1}{2}$ is the same as $\frac{7}{2}$ ?

The whole number part is three. Ask how many halves make up three wholes? Well, one whole has two halves, so three wholes have 3 x 2 or 6 halves.

With another half to add, this gives us 7 halves, or $\frac{7}{2}$ .

Conversely, for converting improper fractions to mixed numbers, divide the numerator by the denominator.

7 divided by 2 is three with a remainder of one. So, $\frac{7}{2}$ is 3 wholes with 1 half or, $3\frac{1}{2}$ .

These conversions are handy in both academics and everyday life. Whether splitting a pizza into more practical slices or calculating an ingredient in baking, recognizing whether a mixed number or improper fraction is more useful is key.

A helpful practice is to work with these numbers in tangible examples. Here, 7 blue discs represent 7 pizzas:

Sharing them between two people, each receives three whole pizzas – three yellow and three red with one left as blue.

To be shared between two people, the remaining blue disc must be cut in half. So, 7 pizzas shared between two people sees each person received three and a half pizzas or $3\frac{1}{2}$ .

Equally, each of the seven pizzas could have been cut into two pieces. This would result in 14 halves.

When 14 is shared between two, each person would receive 7 halves or $\frac{7}{2}$ .

Understanding and being able to convert between these different ways of writing fractions builds a stronger foundation in maths. In turn, confidence when solving problems is enhanced, where these different forms appear. Practising these skills helps them become second nature, simplifying many numerical challenges along the way.

Comparing Fractions and Decimals

With a good grasp on mixed numbers and improper fractions, the next skill is comparing fractions and decimals. This skill is important for making accurate judgments in practical scenarios, like budgeting or measuring.

When dealing with fractions, it’s often necessary to have a common denominator to make comparisons easier. For example, deciding if $\frac{3}{4}$ is larger than $\frac{2}{3}$ is best done by converting them to have the same denominator.

In this case, the fractions become $\frac{9}{12}$ and $\frac{8}{12}$ , respectively. Once they share this basis, it’s clear which is larger.

For decimals, it’s much like comparing whole numbers. Perhaps the decimal point causes confusion. However, if they are lined up in their place value columns, the decimal point can be ignored.

Then, compare the digits place by place. For instance, comparing 0.75 and 0.8 involves noting the 8 in the tenths place is more than 7, making 0.8 the larger number.

Sometimes these comparisons involve both fractions and decimals. It is best to convert so they are in the same format. With consistent practise and experience, learners can see how numbers compare. Also, visualisation tools, like number lines, can be of great use when trying to understand these comparisons.

Another way in to compare is to use money. For example, which is greater, £0.75, or £0.80? If we consider that £0.75 is 75p and £0.80 is 80p we can see easily that 80p is greater than 75p. Practicing real-world comparisons can make them less daunting.

By regularly comparing fractions and decimals, you deepen your understanding and sharpen your problem-solving toolkit, essential for navigating numerous life situations with confidence.

Adding and Subtracting Fractions – No Simple Task

Now that you’re familiar with comparing fractions and decimals, let’s delve into adding and subtracting fractions. These are essential operations, especially in scenarios where you need to combine or divide things equally.

To add or subtract fractions, they must have a common denominator. For example, to add $\frac{1}{4}$ and $\frac{1}{3}$ , you’d convert them into equivalent fractions with the same denominator.

In this case, we’d choose 12 as the common denominator. $\frac{1}{4}$ becomes $\frac{3}{12}$ and $\frac{1}{3}$ becomes $\frac{4}{12}$ . Since 3 + 4 = 7, the sum of the two fractions is $\frac{7}{12}$ .

Finding a common multiple that both denominators share can sometimes be a puzzle. However, it gets easier with practise. Using the lowest common multiple (LCM) is a smart way to ensure you get there efficiently.

Finding the LCM

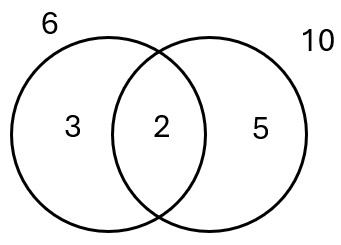
Taking the example of 6 and 10. You would not be wrong to multiply them together (6 x 10) to find a common multiple (60). However, 60 is not the lowest common multiple of 6 and 10. Using 60 would necessitate the simplification of any answer. Using

To find this, first write out 6 and 10 as products of their prime factors.

6 = 2 x 3 and

10 = 2 x 5

Putting these prime factors into a Venn diagram we can see that that 2 is common to both. As a result, the LCM is 3 x 2 x 5 which equals 30.

Once you’ve got those common denominators, you can easily perform the addition or subtraction and simplify the result if necessary. In the above example, even using 30 rather than 60 may require this. Simplifying fractions makes them easier to understand.

A strategic tip: Use visual aids like fraction bars or circles as tools when beginning to understand this concept. They help in visually breaking down the problem until you’re comfortable enough to do it in your head.

Adding and subtracting fractions is a practical skill. It is directly applicable to everyday needs. As a result, precision with these calculations is important. Learners need to practise consistently and tackle different problems.

Multiplying and Dividing Fractions – Not As Tough As You Might Think

Bizarrely, the challenge of multiplying and dividing fractions is not as complicated as adding and subtracting them. This is because there is no requirement to convert fractions to have common denominators.

That said, carrying out these operations expands your toolkit significantly, letting you tackle more complex problems. It is useful, but not essential, to be able to understand what is going on when dividing and multiplying.

Understanding what is happening helps learners become comfortable with carrying out these calculations and prevents them from forgetting how they are done.

Multiplication

When we have a multiplication like $\frac{1}{2}\times\frac{3}{4}$ it can be thought of as what is half of $\frac{3}{4}$ ? Alternatively, it could be what is three-quarters of a $\frac{1}{2}$ ?

To carry out the calculation, multiply the numerators together and the denominators together. As a result, $\frac{1}{2}\times\frac{3}{4}$ = $\frac{1 \times 3}{2 \times 4}$ = $\frac{3}{8}$ .

If needs to be, the answer should be simplified. Three-eights, cannot be simplified. 3 is a prime number and 8 does not appear in the 3x table.

Division

When dividing, it’s as simple as flipping the second fraction and then multiplying it by the first. Using the same two fractions as our multiplication example we get, $\frac{1}{2}\div\frac{3}{4}$ which becomes $\frac{1}{2}\times\frac{4}{3}$ = $\frac{1 \times 4}{2 \times 3}$ .

This gives us the answer $\frac{4}{6}$ . This can be simplified as both 4 and 6 can be divided by 2, so the simplified answer is $\frac{2}{3}$ .

These skills are really useful in the context of scaling up recipes or adjusting the size of a project. If you’re working on something and need to calculate parts of parts, these operations enable you to do it accurately.

Practicing these operations with real-world examples helps solidify the concepts. Try visual aids to start, with fraction strips or pie charts to see how these operations work in action.

Multiplying Decimals

For decimals, multiplying is no different to multiplying numbers without decimal points. It is important that an estimate is made before hand, so that you know where the decimal point will go in the answer.

For example, to multiply 1.5 by 2.3, first simplify the question to either 1.5 x 2 = 3 or 1.5 x 3 = 4.5

This gives a range for your answer of between 3 and 4.5. Alternatively, count the number of digits after the decimal points – 2. Then, make sure your answer has two digits after the decimal place.

Multiplying 15 by 23 gives the answer of 345. Cleary this is not the required answer, because it is outside the range of 3 and 4.5. Neither does it have any digits after the decimal point.

So, adjusting the decimal point in your answer to make it fit in the required range and maintain those two decimal places, results in 3.45

Incorporating these more complex operations boosts your mathematical maturity, enabling you to efficiently solve varied problems. Continual practice in practical situations enhances this skill effectively.

Fractions, Decimals, and Percentages

Rounding off our understanding of fractions and decimals requires grasping the ingenious link to percentages. These three types of numerical representations are different faces of the same concept.

Here we have the holy trinity of parts of the whole. We have seen how to convert between fractions and decimals. Now we will discuss how to convert decimals into fractions and then, fractions into percentages and decimals into percentages and vice versa.

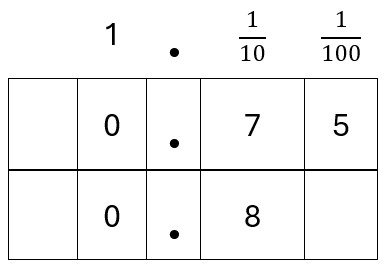
Here are the column headings for two decimal places.:

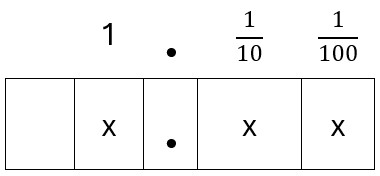
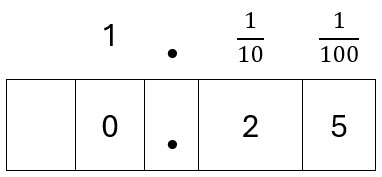
Let’s take a decimal, say 0.25.

Putting it in the grid, shows us that 0.25 is $\frac{2}{10}$ + $\frac{5}{100}$ .

In order to add $\frac{2}{10}$ and $\frac{5}{100}$ we need to have a common denominator. The easiest common denominator is 100. This only requires us to change the tenths into hundredths – $\frac{2}{10}$ = $\frac{20}{100}$ .

In total, $\frac{2}{10}$ + $\frac{5}{100}$ makes $\frac{25}{100}$ . This can be simplified by spotting that 4 x 25 makes 100, so $\frac{25}{100}$ = $\frac{1}{4}$ .

This means that 0.25 is the decimal equivalent of a quarter.

Converting Into Percentages

Splitting the word percent gives us “per” which requires us to divide and “cent” which suggests the number 100. So, a percentage represents a fraction of 100.

For example, 7 percent is $\frac{7}{100}$ and $\frac{23}{100}$ is 23 percent. To convert fractions that are not expressed as tenths or hundredths, it is necessary to convert them into decimals first by dividing.

By the same token, using our place value grid, we can see that $\frac{7}{100}$ is 7 hundredths or 0.07. Similarly, $\frac{23}{100}$ is 0.23.

To summarise,

7% = $\frac{7}{100}$ = 0.07

23% = $\frac{23}{100}$ = 0.23

We have a little more work to do when our fractions are not expressed as tenths or hundredths. In this case, we need either to convert them to equivalent fractions with tenths or hundredths and then express them using place value before following the previous example.

If they are not easily convertible to decimals then they need to be divided using bus stop. This automatically renders them as decimals which can then easily be read as percentages.

Conversion Table For Common Fractions into Decimals and Percentages

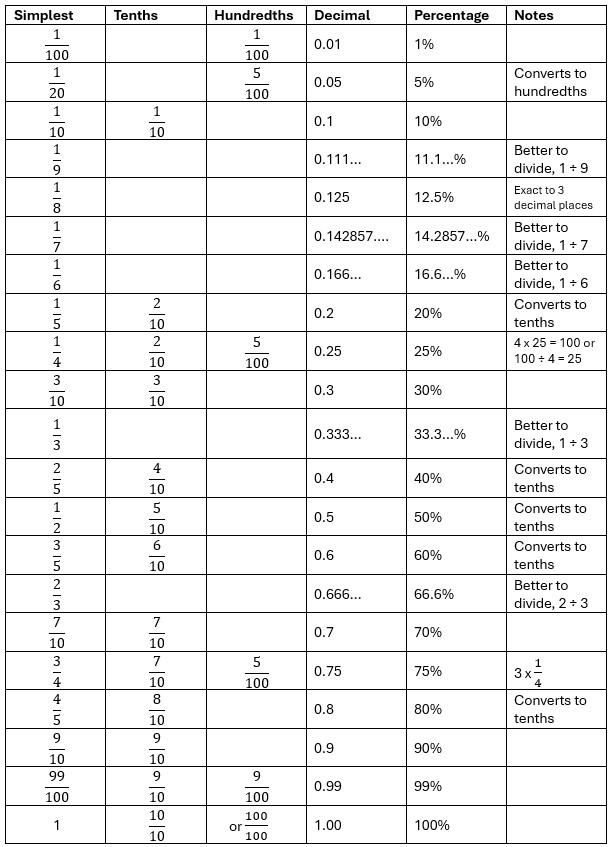
In the table, several conversions from fractions to decimals into percentages are best found by dividing. For example, $\frac{1}{7}$ results in a decimal that is 0.142857142857… with the digits 142857 repeating themselves continuously.

The others in this category are $\frac{1}{9}$ , $\frac{1}{6}$ , $\frac{1}{3}$ and $\frac{2}{3}$ . They are all recurring decimals. This means that digits after the decimal point repeat themselves, either in a patterns as for $\frac{1}{7}$ or perhaps the same single digit. For example, $\frac{1}{3}$ = 0.33333… – nought point three recurring.

In the case of these fractions, there is no exact decimal conversion – all are rounded.

$\frac{1}{8}$ is an interesting fraction because it extends to three decimal places when it is divided. It’s $\frac{1}{10}$ , $\frac{2}{100}$ and $\frac{5}{1000}$ , giving a decimal of exactly 0.125 and a percentage of exactly 12.5%.

Another way of looking is that $\frac{1}{8}$ is a half of $\frac{1}{4}$ . 12.5 is half of 25, so 12.5% is half of 25%.

There are so many ways in to understanding the relationships between fractions, decimals and percentages that the topic merits a whole article on itself. It is sufficient to say that a good grasp of number will assist learners greatly in developing their own pathways to make those links.

My last comment on the matter is to point out that percentages are found by multiplying the decimal equivalent of a fraction by 100(%).

Working with percentages is incredibly practical. Think about discounts while shopping or calculating tips at a restaurant. The real-world application can be understood. Consider calculating a 20% tip on a £50 restaurant bill.

20% is a fifth ( $\frac{1}{5}$ ), so to calculate we divide by 5, or multiply by 0.2. Reassuringly, both result in £10.

With those fractions that don’t correspond to exact decimals, we are required to round them. Even rounding to the nearest tenth or hundredth can affect percentages, influencing decision-making in financial contexts and assessments. Understanding this enables us to navigate offers, interests, and comparative evaluations.

Apply these skills in varied scenarios to build robust confidence. Practice converting real-life examples to see their percentage, fraction, and decimal forms as this practice ensures a more comprehensive grasp and adaptability.

By connecting these concepts, you open up an ability to cross-reference and translate between numerical forms effortlessly, rounding off a comprehensive understanding that enriches everyday problem-solving.

Conclusion

Fractions! The very word has the capacity to strike fear into the stoutest of hearts. But fear not, dear reader. I hope that I have given you an insight into the murky world of fractions. If in doubt, refer back to the model of a fraction I presented right the the start.

Remember, it’s a number on top and a number on the bottom. There’s a line in between that means divide. The bottom number tells us how many equal parts the whole has been divided into. The number on the top tells us how many of those parts are are considering.

To all intents and purposes, that line in the middle can be ignored most of the time. But don’t forget it, sometimes it comes in useful.

At the end of the day, fractions, decimals, and percentages are interconnected ways to represent parts of a whole. Fractions express ratios (parts out of total). Decimals use our base-10 place value grid. Percentages denote parts per hundred.

Converting between them ensures we can compare, calculate, solve problems in maths, science, and finance. Mastery of these concepts is essential for real-world applications.