Introduction to Geometric Concepts in Mathematics
Positional Geometry is perhaps the most practical of all the branches of maths. The study of positions, directions, and movements. It enables us to navigate from A to B and beyond. This exploration begins with ordering and arranging combinations of mathematical objects in patterns and sequences.

Next, it’s about rotations in terms of quarter turns (90°), half turns (180°), three-quarter turns (270°) and full-turns (360°). This is quickly followed by the use of Cartesian coordinates across all quadrants. First, it’s just plotting points and shapes, but it quickly becomes describing positions on a 2-D grid. Then, it’s about representing shapes after reflections or translations and generally articulating movements and navigating the quadrants with increasing sophistication.
Order and arrange combinations of mathematical objects in patterns and sequences
This is an early skill to master for learners. It’s a bridge between shape geometry and positional geometry. Learners are required to study and then continue patterns of shapes.

It may be that the shapes are 2D or 3D. The point is that the exercise offers great opportunities for discussion. Firstly, about which shape, or shapes may or may not follow from the original. Secondly, there is a great opportunity to discuss the properties of the shapes themselves.
Position and direction – quarter, half, three-quarter and whole turns
Next, we come to discussion of turns or rotations. There is another link with the geometry of shapes too, in the use of angles.
Without further ado, you may ask, “What’s a quarter turn?” This is a great opportunity for movement and rich discussion. Perhaps start by facing a window. Then turn through a right angle to face a wall. If you have turned clockwise, the window will be on your left. Explain that you have turned a right angle or 90° or a quarter turn.
Turning another right angle or another 90° means that you have turned through a total of 180° or half of a full turn. Talk about where the window that you started off facing is now. If you’ve done it correctly, it will be behind you.
Turning another right angle means that you have turned through a total of 270° or three-quarters of a full turn. Presuming that you turned clockwise originally, the window will now be on your right.
Finally, make that final quarter turn and you will have made a full turn; that’s your whole 360°. You have turned through a full circle and should now be facing that window again.
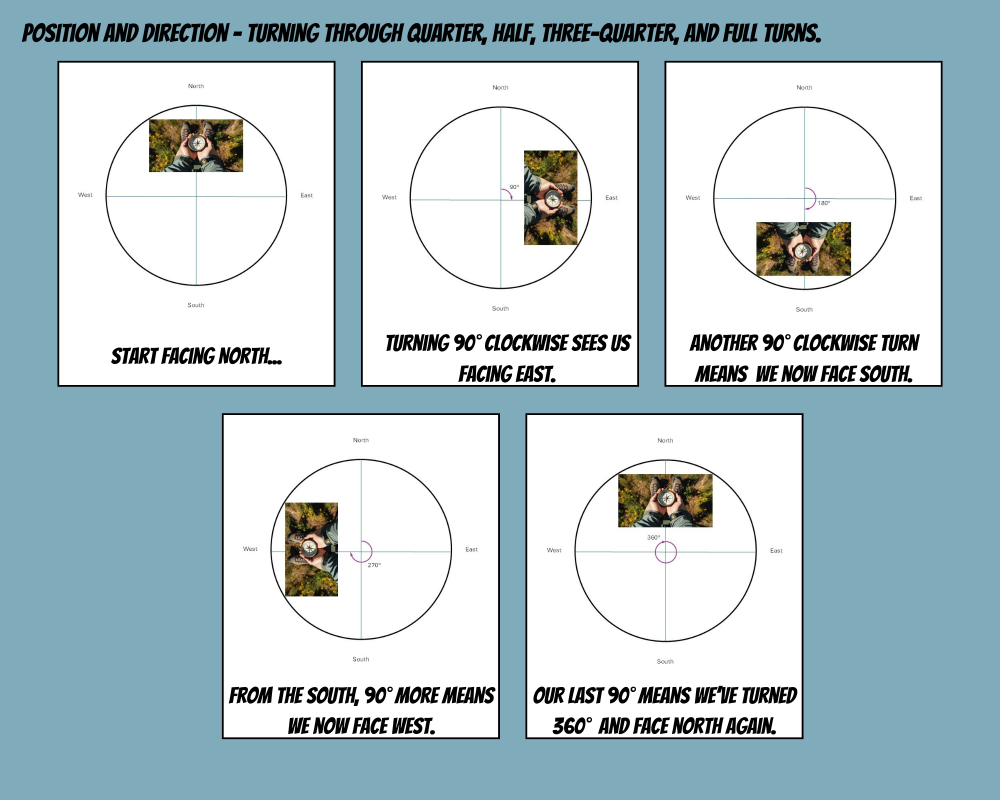
There are several applications of understanding turns. For example, points on a compass. Presuming that the window you start off facing is north, your first quarter turn means that you then face to the east. Half a turn means that you face south. Another turn of 90° sees you facing west before your final quarter turn sees you once again facing north.
Use of Cartesian coordinates. Starting from the first quadrant but progressing to all four.
Don’t worry about the term Cartesian coordinates. This section is just about those x- and y-axes. From your school days you may rememberthe phrase “Along the corridor, and up the stairs.” This is a quick ditty to help us remember that to use Cartesian coordinates (or just coordinates), we quote the x-coordinate first, then the y-coordinate.
Picture a treasure map overlaid with a grid. Each line on the grid will be numbered, and consequently, each intersection can be referenced by its x- and y-coordinates. That way, a big X marked on the map can be referenced by its coordinates.
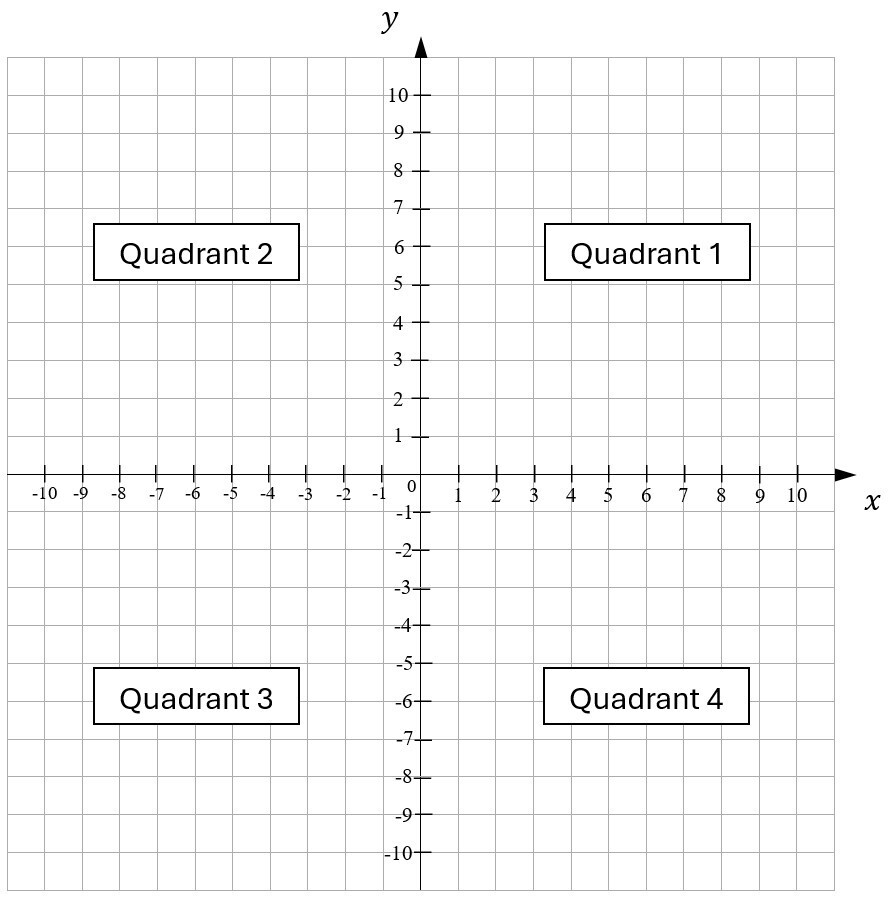
Initially, learners will work with coordinates in the first quadrant only. In this quadrant, both the x- and y-coordinates are positive. Later, learners will start to use all four quadrants when x and y could be positive or negative.
Coordinates are the basis of maps and mapping. Since one purpose of maps is to help us move from A to B, one of the first things we do with coordinates is to practice making simple moves. So, it will be right or left across the x-axis and up or down along the Y-axis.
Coordinates pop up in many other real-life applications. In addition to being able to move from A to B, architects, planners, and builders use them to decide where new developments should be located. GPS is nothing without coordinates.
Describe movements using increasingly sophisticated language – from up/down and left/right towards translations and reflections
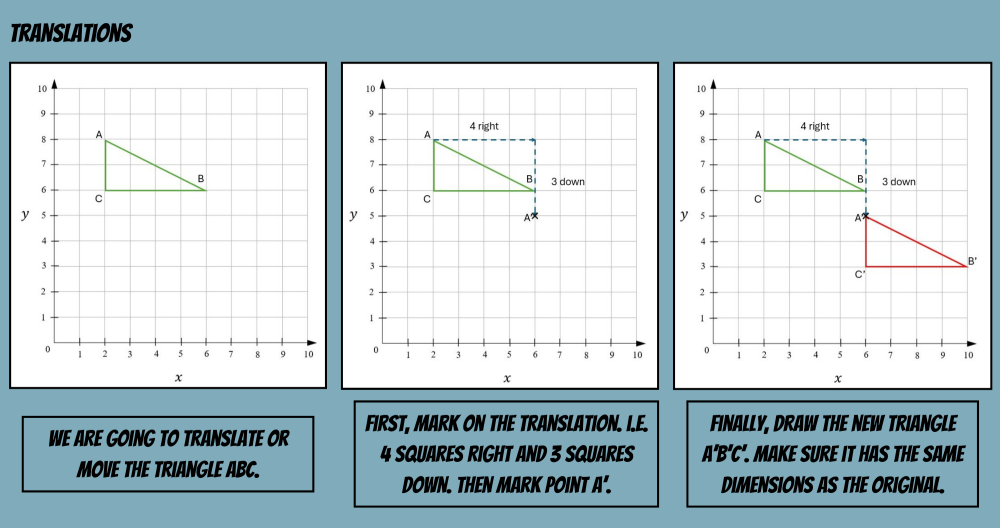
Translations slide shapes, moving them around without altering their appearance. They may be moved by a given pair of steps – e.g. 2 to the left and 4 up. Alternatively, a shape may be drawn with a vertex marked and the instruction to redraw the shape with the seme vertex marked at another coordinate.
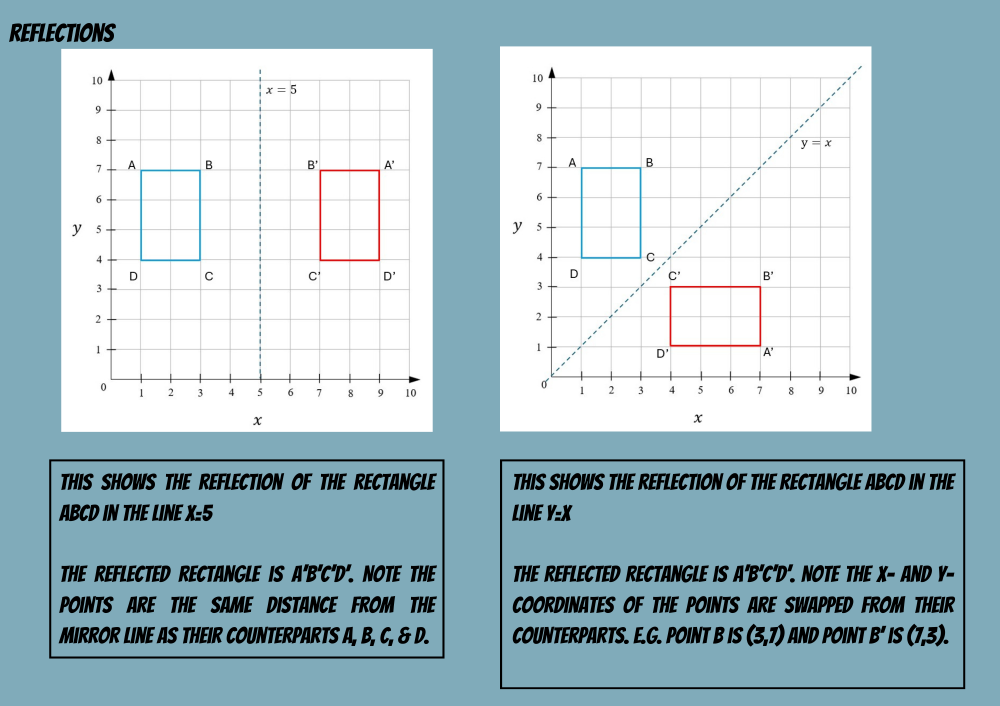
Reflections flip objects, creating mirror images. Shapes may be reflected in a mirror line which is drawn, or they may be reflected in either the x- or the y-axis.
The directions required to describe translations require clear and precise language. As well as those movements themselves, they also help sharpen learners’ ability to communicate complex ideas.
Plot specified points and draw sides to complete a given polygon
This discipline pulls together several other skills. Learners need to know how to plot points on a grid, and they need to know the properties of the polygons they are required to complete.

Precision matters. Points must be plotted in the correct place. If a point is misplaced, a wobbly polygon may result. Patience and attention to detail are required.
Understanding which polygon is required and visualising it plays a big role in enhancing spatial reasoning. These skills extend beyond mathematics. They have applications in everything from crafting creative designs to solving practical architectural problems. As learners master plotting and drawing, the navigation of other geometric challenges and real-world tasks becomes significantly less daunting.
Connecting Geometry to Everyday Experiences
Geometry is an applied maths skill. It is more than numbers and shapes on a page. Having a good grasp of geometry can enhance everyday problem-solving and foster creativity.
Geometry’s patterns and sequences, Cartesian coordinates and polygons inform the world around us. From the built environment, through art and design, to the symmetry of a butterfly’s wings or the sleek design of a smartphone, all are founded upon geometric foundations.
Geometry helps develop analytical skills and problem solving – abilities that are valuable across various fields. Geometry instils a mindset that notices the elegance and simplicity of mathematical relationships in the everyday.

