Taken literally, the word geometry means to measure the Earth. It is the study of the properties and relations of points, lines, surfaces (2D shapes) and solids (3D shapes).

Shapes
The first topic, appropriately, concerns shapes. Under this heading, learners cover the following aspects:
Recognising and naming 2D and 3D shapes
This may not come as a surprise, but shapes are the basis of the whole topic. Learners are taught how to describe their properties. New words include:
Sides – the lines drawn to form a 2D shape (polygon)
Angles – these are formed when lines cross or meet at a point. The amount of turn between the two lines is measured in degrees (°).
Symmetry – if match were folded in half and the halves match exactly, it is said to be symmetrical
Face – a surface of a 3D shape, formed from a 2D shape
Edges – the line along which two faces of a 3D shape are joined
Vertex (plural vertices) – the point where two lines meet in a 2D shape; or the point on a 3D shape where three edges or more meet.
2D Shapes
Using this knowledge, they are then encouraged to compare and classify them. Using dimensions and angles, 2D shapes can be drawn.
Next, learners begin to distinguish between regular and irregular polygons. Prior learning, i.e. the distinction between each, helps them to do this.
A regular polygon has all its sides and angles the same. For example, a square is a regular quadrilateral, but a rectangle is not. Because we don’t usually refer to a square or a rectangle as anything else, it might seem silly to use these as examples. However, I think it is thought-provoking when learners hear them referred to as such.
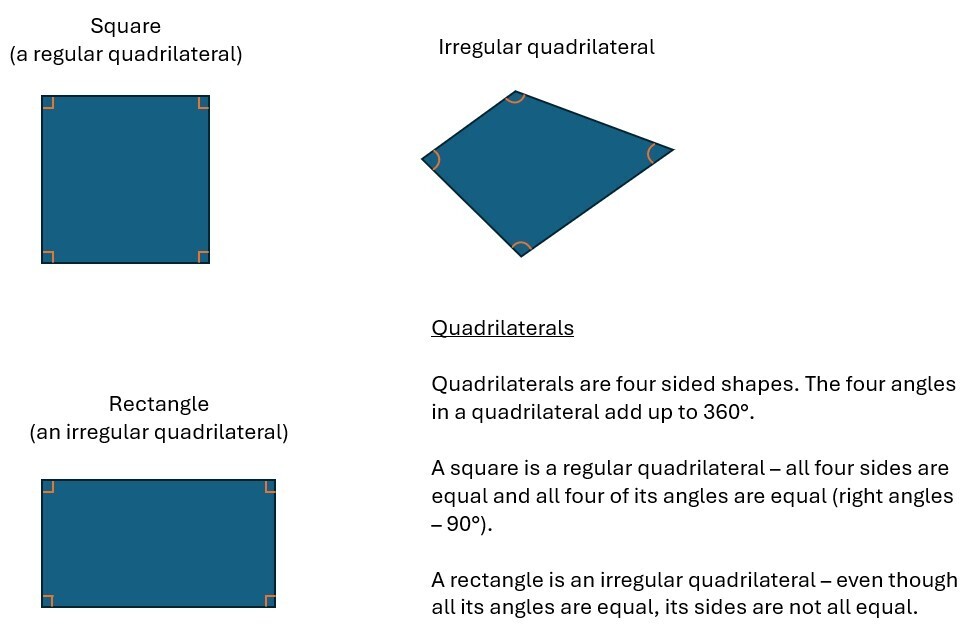
“What? A square is a regular quadrilateral?”
“Yes, and a rectangle is an irregular quadrilateral.”
Applying Knowledge of The Properties of Shapes
Once learners know the properties of triangles, quadrilaterals and regular polygons, they can begin to work on finding unknown lengths and angles in them. It may come as a surprise, but in carrying out these questions, learners use algebra. Of course, it is not explicitly referred to as such.
3D Shapes
Next, we move on to 3D shapes. Initially, learners are taught how to recognise and describe them. New terms like edges, vertices, and faces are introduced into learners’ vocabulary.

A great way to help consolidate knowledge of 3D shapes is to build them from what are called nets. This is a great way of seeing and consolidating how these 2D shapes are put together as the faces of 3D shapes.
Circles
Circles are a sub-group of shapes that are given considerable coverage in later maths. For now, learners will learn about the simpler parts of a circle. Radius, diameter and circumference.
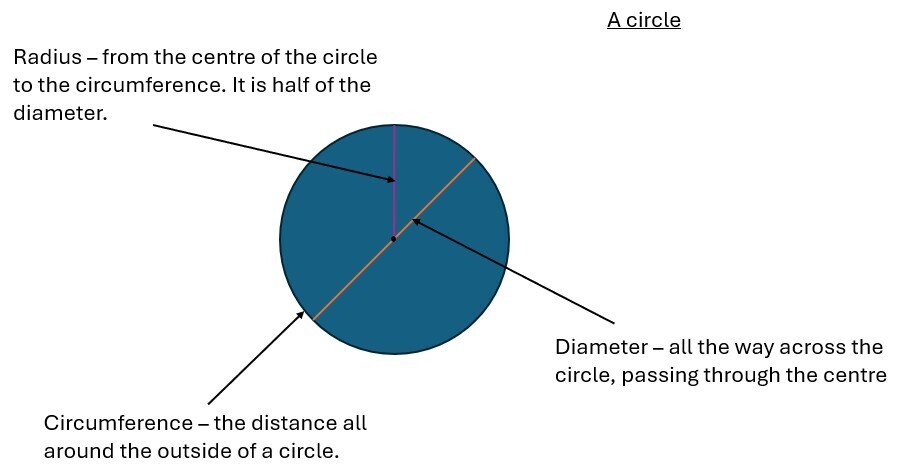
Mention is made of Pi, the ratio of any circle’s circumference to its diameter. It is also noted that the diameter of a circle is twice its radius.
Angles
Measured in degrees (°), angles have a couple of definitions. They can be either a property of a shape or a description of a turn. In both instances, they are formed by two lines joining at a point or vertex.
For angles in a shape, these lines are visible. Angles made by turning are better drawn in so that they can be seen, although, in real-life applications, they are generally not visible.
An important angle for learners to identify is a right angle. A right angle measures exactly ninety degrees (90°). When considering shapes, right angles are most associated with squares and rectangles.
Of course, right-angled triangles are the basis for two areas of study in later maths, namely Pythagoras’ Theory and trigonometry.
Learners need to be able to compare angles to a right angle. This enables them to identify acute and obtuse angles. Acute angles are smaller than a right angle, and obtuse angles measure between 91° and 179°. Reflex angles are between 181° and 359°.
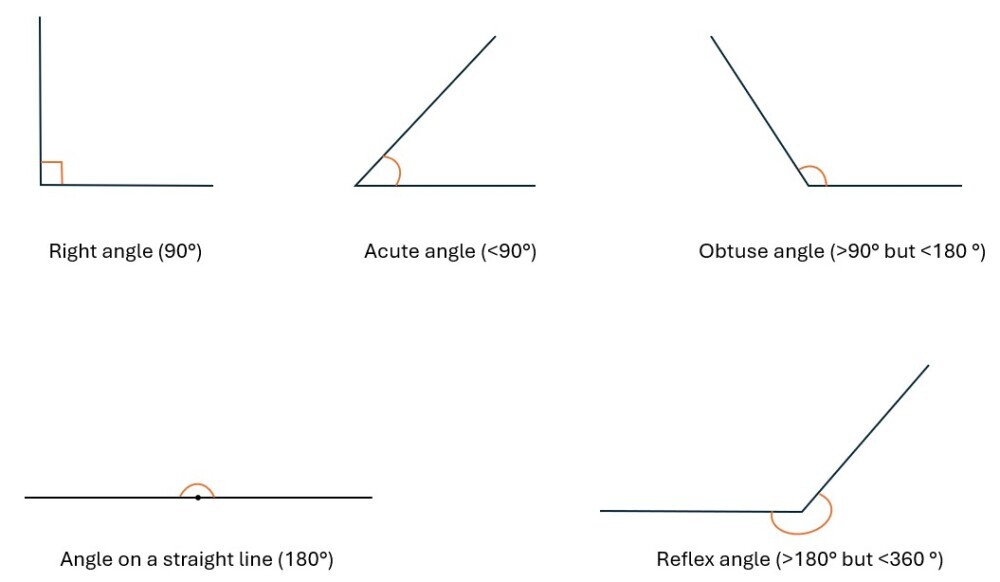
Learners need to be able to estimate and compare acute, obtuse and reflex angles. They also should draw and measure angles. This will require the use of a protractor.
When turns are considered, a right angle is a quarter turn, and two right angles (180°) make a half turn (straight line). Three right angles make a three-quarter turn (270°) and four make a complete turn (360°).
Angles Formed by Lines and Angles as Turns
The angles at a point add up to 360° – a whole turn. Furthermore, the angles on a straight line (a half turn) add up to 180°.
When two straight lines cross four angles are made. Together they total 360°. Each pair of opposite angles, known as vertically opposite angles, are equal. Each pair of adjacent angles add to a total of 180°.
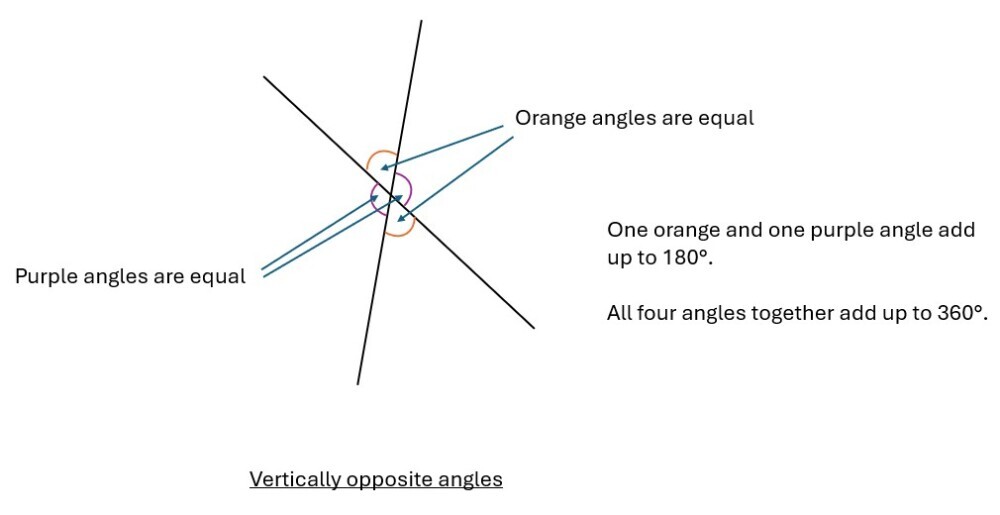
Using this information, learners will progress to finding missing angles in problems that are presented.
Parallel and perpendicular
Learners identify vertical, horizontal, parallel and perpendicular lines. Vertical lines run up and down. Horizontal lines run from right to left – remember that the sun rises above or falls below the horizon. The horizon is a horizontal line in the distance.
To describe parallel lines, I think of a pair of railway lines. They run together but never meet. They are always precisely the same distance apart.
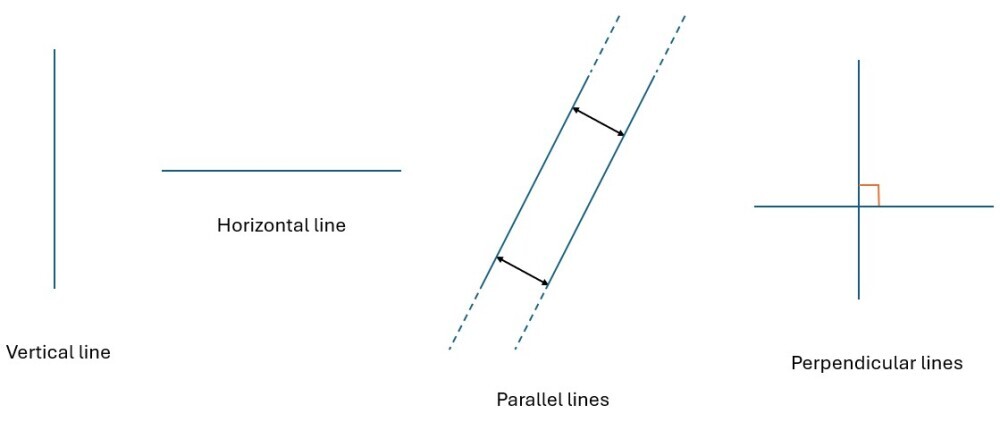
Perpendicular lines are lines that meet (or intersect) and form a right angle as they do. For example, a horizontal line and a vertical line would be perpendicular should they meet or intersect.
Symmetry
In KS2 geometry, symmetry is taken to mean reflective or line symmetry. A shape is symmetrical if it can be divided into at least two identical parts that are reflections of each other. i.e. each half is a mirror image of its twin.
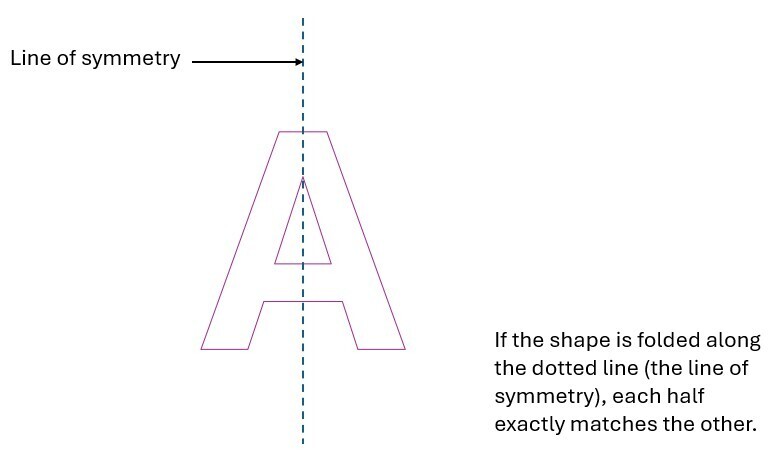
In later maths, it is also observed as rotational symmetry, where an object looks the same after a certain amount of rotation.
Learners can practise their line symmetry skills by completing a simple symmetric figure when given a specific line of symmetry to reflect. For example, they might be tasked with reflecting a shape over a mirror line to create a symmetrical figure.
If presented on squared paper, squares help them visualise what the shape would look like. I.e. by paying attention to how many squares away from the mirror line each vertex of the shape is.
