Learning tables
Times tables are fundamental maths facts. It is very difficult to be confident and do maths well if they are not known. Not knowing them causes anxiety and even resentment. Traditional methods may drill the facts into learners, but they don’t always stick and offer no way of ‘working out’ the answers.
I would argue that a better and more secure way to learn tables is to come from the point of view of having a good understanding of number. It is no accident that the five times table is included within the first group of three tables to be learnt.
The Five Times Table
The five times tables has a simple rhythm when it is recited. The last digit (digit in the Ones place) end alternatively 0, 5, 0, 5… Those ending in zero are answers in the ten times table too – hold your hands up and you can see 2 groups of 5 making ten.
The Ten Times Table
On the face of it, multiplying by ten is simple. You just add a zero on the end. Well, yes – for whole numbers, in effect that’s what you do. Reality is slightly more complicated.
When multiplying by ten, the digit moves one place to the left, e.g. 3 x 10 sees the 3 move from the Ones column to the Tens column. The space that is left in the Ones column must be filled, and it is filled with a zero. This is why the answers in the ten times table always have a zero in the Ones place. Or put a
The Two Times Table
On the face of it, multiplying by 2 is simple enough. Pairs of objects are all around us –
- Two hands each with 5 fingers totals 10 fingers 5 + 5 = 10
- Two wheels on each axel of a car totals 4 wheels 2 + 2 = 4
- Two rows of three eggs in an egg box gives a total of 6 eggs 3 + 3 = 6 or
- Two rows of six eggs in a larger egg box gives a total of 12 eggs 6 + 6 = 12
We can tap into this to help our children double – two groups of the same thing or add two of the same quantity together. I would caution not to assume that the two times table is easy – try counting in groups of ‘b’ in the alphabet…
Support your child with the use of representations like the ones mentioned above. Use pairs of objects to model doubling.
The Three Times Table
Recalling that multiplication is repeated addition is a good way to learn the three times table. The numbers in the three times table are not that large, so this method of counting on works well in the first instance.
Later, the fact that 3 = 2 + 1 can be used to help. Three times something is double that number, plus one more group of the number.
For example,
- 3 x 4 = double 4 plus 4 = 8 + 4 = 12
- 3 x 5 = double 5 plus 5 = 10 + 5 = 15
- 3 x 7 = double 7 plus 7 = 14 + 7 = 21
The Four Times Table and the Eight Times Table
Using the fact that 4 is double 2 and that 8 is double 4 helps greatly with learning the fours and the eights. Every other answer in the two times table is found in the 4s and every other answer in the 4s is found in the 8s.
| 2x | 4x | 8x |
| 2 | 4 | 8 |
| 4 | 8 | 16 |
| 6 | 12 | 24 |
| 8 | 16 | 32 |
| 10 | 20 | 40 |
| 12 | 24 | 48 |
| 14 | 28 | 56 |
| 16 | 32 | 64 |
| 18 | 36 | 72 |
| 20 | 40 | 80 |
| 22 | 44 | 88 |
| 24 | 48 | 96 |
By the time children have learned the 2x, 3x, 4x, 5x, 8x, and 10x tables in theory there’s not a great number of fresh facts to learn. This is because like addition, multiplication can be carried out in any order. In all the ‘new’ tables, we can already carry out most of the necessary calculations.
The Six Times Table
Taking a leaf from learning the 4x and 8x tables, the 6x table can be grasped relatively quickly by doubling the facts in the 3x table.
| 3x | 6x |
| 3 | 6 |
| 6 | 12 |
| 9 | 18 |
| 12 | 24 |
| 15 | 30 |
| 18 | 36 |
| 21 | 42 |
| 24 | 48 |
| 27 | 54 |
| 30 | 60 |
| 33 | 66 |
| 36 | 72 |
The Seven Times Table
It must be said that the 7x table sounds horrific. But due to the nature of multiplication, there are only a handful of new facts to learn. For example, children already know double 7. Three sevens is double 7 plus 7. Four sevens are double 14, 5 sevens is 35.
This leaves 6 x 7 = 42, 7 x 7 = 49. 8 x 7 can be worked out from doubling 28. 9 x 7 could be thought of as 10 x 7 with 7 subtracted.
The Nine Times Table
There is a nice pattern to the 9x table. Starting with 1 x 9 = 9, as the Tens count up by one each time, the Ones reduce by one. The 9x table may also be thought of the 10x table with one group of the number subtracted.
| Digit Sum | Using 10x | ||
| 1 x 9 = | 9 | 9 | (1 x 10) – 1 |
| 2 x 9 = | 18 | 9 | (2 x 10) – 2 |
| 3 x 9 = | 27 | 9 | (3 x 10) – 3 |
| 4 x 9 = | 36 | 9 | (4 x 10) – 4 |
| 5 x 9 = | 45 | 9 | (5 x 10) – 5 |
| 6 x 9 = | 54 | 9 | (6 x 10) – 6 |
| 7 x 9 = | 63 | 9 | (7 x 10) – 7 |
| 8 x 9 = | 72 | 9 | (8 x 10) – 8 |
| 9 x 9 = | 81 | 9 | (9 x 10) – 9 |
| 10 x 9 = | 90 | 9 | (10 x 10) – 10 |
| 11 x 9 = | 99 | 18 | (11 x 10) – 11 |
| 12 x 9 = | 108 | 9 | (12 x 10) – 12 |
The Eleven Times Table
This is a relatively straightforward table to learn. Up to 9 x 11 the answers repeat the other factor. For example,
- 2 x 11 = 22
- 3 x 11 = 33 etc.
10 x 11 is 11 with a zero tagged on the end. 11 x 11 and 12 x 11 need to be learnt – but can be done so by adding ten and then one more.
- 11 x 11 = 110 + 10 + 1 = 121
- 12 x 11 = 121 + 10 + 1 = 132
The Twelve Times Table
The fact that 12 is 10 plus 2 can aid in learning the 12x table.
| 10x | 2x | 12x | |||||
| 1 x 12 = | 1 x 10 | + | 1 x 2 = | 10 | + | 2 = | 12 |
| 2 x 12 = | 2 x 10 | + | 2 x 2 = | 20 | + | 4 = | 24 |
| 3 x 12 = | 3 x 10 | + | 3 x 2 = | 30 | + | 6 = | 36 |
| 4 x 12 = | 4 x 10 | + | 4 x 2 = | 40 | + | 8 = | 48 |
| 5 x 12 = | 5 x 10 | + | 5 x 2 = | 50 | + | 10 = | 60 |
| 6 x 12 = | 6 x 10 | + | 6 x 2 = | 60 | + | 12 = | 72 |
| 7 x 12 = | 7 x 10 | + | 7 x 2 = | 70 | + | 14 = | 84 |
| 8 x 12 = | 8 x 10 | + | 8 x 2 = | 80 | + | 16 = | 96 |
| 9 x 12 = | 9 x 10 | + | 9 x 2 = | 90 | + | 18 = | 108 |
| 10 x 12 = | 10 x 10 | + | 10 x 2 = | 100 | + | 20 = | 120 |
| 11 x 12 = | 11 x 10 | + | 11 x 2 = | 110 | + | 22 = | 132 |
| 12 x 12 = | 12 x 10 | + | 12 x 2 = | 120 | + | 24 = | 144 |
Identify multiples and factors, incl. finding factor pairs
Next, we come to identifying multiples and factors. Multiples are the answers in a times table whilst factors are the (usually) pairs of numbers that multiply together to give the multiples.
For example, 3 and 4 multiply together to give 12. So, 12 is the multiple and 3 and 4 are factors of 12. There are other factor pairs that make 12. 1 and 12 multiply together to make 12, as do 2 and 6.
Factors and multiples are used in many aspects of not only arithmetic and calculation, but also mathematical structure, equations and operations, fractions and problem solving.
Identify common factors and common multiples
It is important to be able to identify common factors and common multiples. For, when converting fractions to the same denominator to add or subtract, being able to find a common multiple (usually lowest common multiple) is essential.
In the case of simplifying fractions, being able to find a factor common to both numerator and denominator is essential.
Identify prime-numbers and then prime factors
Prime numbers are those numbers with only two factors. For example, 2, 3, 5, 7, 11, 13, 17 and 19 are all prime numbers. They can only be made by multiplying one and themselves. For this reason, 1 is not a prime number because it only has one factor. 2 is the only even number that is a prime number.
If a number is not prime, it is known as a composite number. Prime factors are factors which are prime numbers. All numbers can be broken down into their prime factors. For example, 24 can be calculated by multiplying its prime factors together.
- 24 = 2 x 2 x 2 x 3 or 24 = 23 x 3
Further examples include
- 42 = 2 x 3 x 7
- 51 = 3 x 17
- 60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
Make the link between multiplication and division
In many respects, it is already too late to attempt to make the link between multiplication and division. They are inextricably linked and should be taught together as soon as possible.
Consider multiplication as the putting together of number of groups of a quantity. Division is the breaking apart of larger quantities into a number of groups of a smaller quantity.
For example, 5 groups of 6 makes 30. Similarly, 6 groups of 5 makes 30. When 30 is broken apart into 5 equal groups there are 6 items in each group. If 30 is broken down into 6 equal groups, there will be 5 in each group.
Extend from knowing times tables to multiplying numbers up to four digits using tables and place value knowledge
Multiplication of larger numbers is carried out using a method known as the grid method which eventually gives way to the compact method – a formal written method.
Here’s a set of examples, which become progressively more challenging:
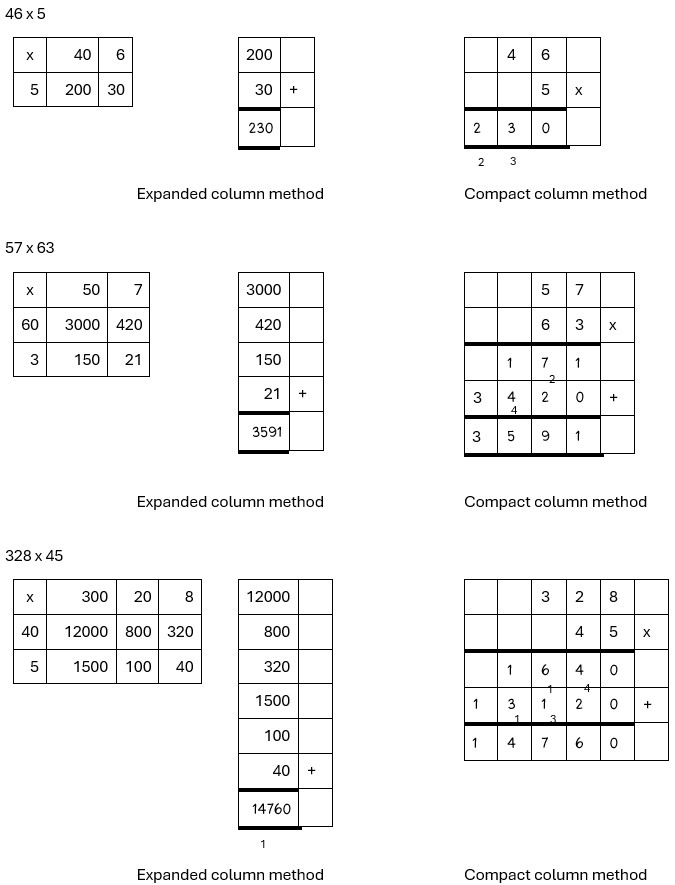
Multiply and divide mentally using known facts
It is desirable that learners become more familiar and comfortable with their times tables knowledge – both multiplication facts and division facts. This will result in their gaining confidence and beginning to find mathematics less difficult. They will have less fear of maths.
Perform mental calculations with larger numbers and mixed operations
This is a further indication of increasing familiarity and confidence with multiplication and division facts and processes.
Divide using short division (bus stop)
This is the traditional method of carrying out division of larger numbers by single digit numbers. In the primary curriculum, the requirement for long division – that is division of larger numbers by two digit numbers, appears only in Year 6.
Two examples of bus stop method – short division.

The next two examples show bus stop method – long division.

Divide and identify remainders as whole numbers or fractions or decimals or by rounding
In early work with division, remainders are expressed as a quantity left over when a division calculation is carried out.
For example, here we see 21 ÷ 4 = 5 r 1

By Years 5 and 6, there is a requirement for remainders to be interpreted either as a fraction or a decimal. In this instance, the remainder 1 is one quarter or 0.25. This is because we have divided by 4 so any remainders are quarters. The full answer is five and a quarter (![]() ) or 5.25
) or 5.25
If the question were 21 ÷ 5, the answer would be 4 and a fifth (![]() ) or 4.2
) or 4.2
Multiply and divide by powers of 10
This is a useful discipline. Our number system is based upon columns of digits, with each column on the left ten times greater in value than its neighbour on the right. Being able to understand what happens in moving between the columns is of great importance.

In later maths, powers of ten are important in expressing numbers which otherwise would contain many zeros using scientific notation.
Understand and use the concepts of square and cube numbers
Square numbers are useful in the learning of times tables. This is despite not being as readily mastered as doubling. They can be learnt by the use of arrays to aid learners in making links between squares of differing sizes and their area. For example,
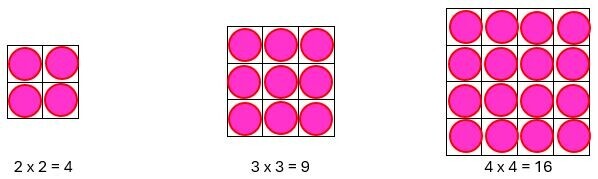
If a square number can be represented by the 2D shape, then ditto for cube numbers with the 3D shape.
Taking the examples above, two cubed or 23 or 2 x 2 x 2 = 8. Similarly, three cubed or 33 or 3 x 3 x 3 = 27. Four cubed, written 43 – 4 x 4 x 4 = 64.
Show commutativity of multiplication
Commutativity means that multiplication calculations can be done in any order. It has at least two benefits for learners. The first one relates to learning the times tables. Thrown by 5 x 7? Commutativity allows you to rewrite the question as 7 x 5. Since the five times table is more straightforward than the seven times table, this removes a lot of stress.
The other benefit of commutativity is being able to reorder multiplications such as 6 x 20. Knowing that 20 is 2 x 10, allows 6 x 20 to be calculated in two steps. 6 x 2 gives 12, and then 12 x 10 = 120.
Use factor pairs, prime factors and commutativity in mental calculations
Using factor pairs, prime factors, and commutativity in mental calculations can significantly simplify complex arithmetic and improve efficiency.
Factor pairs can help break down calculations into smaller, more manageable steps. For example, 36 x 25 could be reorganised to 9 x 4 x 25. Knowing that 4 x 25 = 100 yields the revised, much simpler calculation 9 x 100. This equals 100.
Factor pairs make division easier. For example, in the case of 72 ÷ 8, recognising that 8 x 9 gives the answer 72 allows the answer is 9 to pop out.
Factor pairs allow you to decompose large numbers into smaller, more familiar components.
Prime Factors
As we have seen, prime factorization involves breaking a number into its prime components. This is especially useful for simplifying calculations involving multiplication, division, or finding common denominators.
When simplifying fractions prime factors help reduce fractions to their simplest form.
For example, let’s simplify ![]()
36 has prime factors 2 x 2 x 3 x 3 and 48 has prime factors 2 x 2 x 2 x 2 x 3.
Therefore, ![]() can be written as
can be written as ![]()
Cancelling the common prime factors leaves us with ![]() .
.
This can also be done by recognising that the highest common factor (HCF) of 36 and 48 is 12. 36 = 3 x 12 and 48 = 4 x 12. ![]() can be written as
can be written as ![]() .
.
The two twelves cancel leaving ![]() .
.
Prime factors can make multiplication and division more efficient. Breaking numbers into their primes can make calculations easier.
For example, 168 ÷ 12 can be reduced to 23 x 3 x 7 and 12 reduced to 22 x 3. Cancelling the common prime factors gives us the answer 2 x 7 = 14.
Prime factors are also essential for finding the least common multiple (LCM) or highest common factor (HCF), which simplifies multi-step problems.
Commutativity
As we have seen, the commutative property states that the order of addition or multiplication does not affect the result. This applies to both addition and multiplication. So, leaners should be encouraged to rearrange calculations to make them as straightforward as possible.
For example, if you need to calculate 25 x 24, it is a good idea to note that 24 = 6 x 4. With the knowledge that 4 x 25 = 100, this simplifies the calculation of 25 x 24 to 100 x 6, which equals 600.
Combining These Concepts
These ideas can be used together to make quite complex calculations manageable. For example, the calculation 84 x 75 can be rewritten using factor pairs.
84 = 12 x 7 and 75 = 3 x 25. Breaking down the 12 further to 4 x 3 gives us 84 x 75 = 3 x 4 x 7 x 3 x 25.
Commutativity allows us to rewrite it as 4 x 25 x 3 x 3 x7. This leaves us with 100 x 9 x 7 which in turn reduces to 100 x 63, which is 6300.
So, using factor pairs, prime factors, and commutativity allows us to:
- Break down problems into smaller, simpler steps
- Better arrange numbers for easier calculations
- Solve problems more efficiently and accurately in our head.
Problem solving. Pull together all the aspects of multiplication and division to solve in context
Finally, it must be remembered that maths is a practical subject. Using all of these multiplication and division skills, problems with real life contexts can be solved.
