Usually written in the form: 
, a ratio shows us how two or more quantities are related to each other.
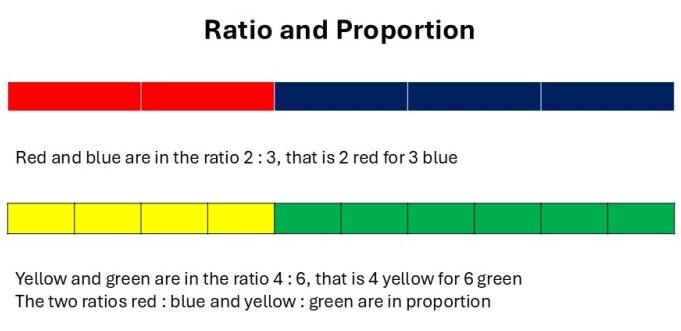
A great way to introduce learners to the topic is with simple scenarios. For example, in a big bag of sweets, there are 2 red sweets for every 3 blue sweets. The relationship between red and blue sweets is the ratio. In this instance, we say the ratio of red to blue sweets is 2:3.
Related to ratio is proportion. It is perhaps most usefully used when scaling ratios up or down. For example, with recipes. As we scale the amounts of things needed, proportion helps us to maintain equal ratios between the ingredients.
Say we are following a cake recipe which calls for 100g of flour, 100g of sugar, 100g of butter and 2 eggs. If we wanted to make 2 cakes, we would need to maintain the ratio between the ingredients. We would need to keep them in proportion.
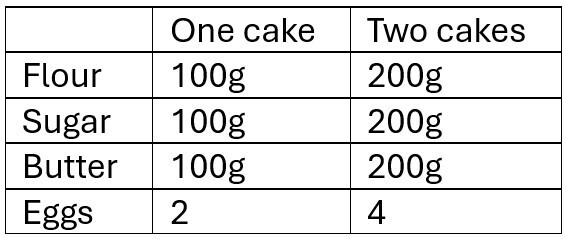
You can see that each quantity is scaled up by a factor of 2 to keep them in the correct proportion.
Problem Solving Using Ratio and Proportion
In school, learners are taught to solve problems involving the relative sizes of two quantities. For example, if one ticket to a pantomime costs £6.50, how much will 4 tickets cost?
They are also shown how to solve problems by calculating percentages and using them for comparison. For example, Sarah bought 20 sweets and eats 25% of them. Her friend Amanda bought 16 sweets and eats 50% of them. Who has more sweets left?
Scale and proportion can also be useful in geometry. Learners are shown how to solve problems involving similar shapes where the scale factor is known or can be worked out.
Finally, problems involving unequal sharing and grouping are solved using knowledge of fractions and multiples. For example, if there are sweets in a bag in the ratio of 3 mini Bounties for every 5 mini Mars Bars, how many mini Mars Bars are there if there are 9 mini Bounties?