This is not so much about why, but more about how you should count with your child. Many of the ideas covered here come from Fosnot & Dolk, 2001.

Maths is a broad topic that has many descriptions. It is all things to all people. I’m going to offer my opinion and say this it is the study of quantity, shape and arrangement. I’m going to go out further onto a limb and say that it is primarily about quantity. Counting, ordering and recording quantities.
Studies have shown (Wynn, 1988) that babies can respond to changes in quantities of things. Very clever, huh? The thing is, they do not do this by counting. They exercise a perceptive skill. They perceive the whole rather than counting the total.
This ability has a technical name – subitising. We all do it to a degree. For example, we can see immediately when we roll a six on a die or how many fingers on one hand someone is holding up.
But anyway, back to those babies. They can perceive magnitude (size), but they have no idea about cardinality, or counting to ascertain the quantity.
Right from the start, we interact with our young children using sing-song talk and chatter. It’s how our parents interacted with us. We recite nursery rhymes. You know the sort of thing. There’s that one about the cat and the fiddle, and the cow jumping over the moon; little dogs laughing, etc.
There’s another one which you may remember, it’s the one about catching a fish and the fish biting your finger. You know:
One, two, three, four, five, once I caught a fish alive,
Six, seven, eight, nine, ten, then I let it go again…
It’s a lovely interaction between parent and child, but is it useful in a maths context? Of course, it helps because your child is hearing the numbers from 1 up to 10. They are becoming familiar with them, along with the order in which they come. So, that’s good.
However, the numbers are abstract – they are not linked to quantity or value. In that sense, they are meaningless.
How to Count With Your Child
Imagine then, counting out objects with your child. You could use anything, from plastic toys to bottle tops, Cheerios to pasta shapes. So long as they are physical objects that can be picked up and put down, counted and grouped.
The key is to link your counting, your recital, of the numbers to the items. We call this one-to-one correspondence. In doing this, you help your child connect the names of numbers with the amounts they represent. This is cardinality. Note that when you stop counting, the last number you say is the total number of items in the set.
Next, we meet another concept with a highfalutin name, hierarchical inclusion. This is the idea that because 1 + 1 = 2, 1 is included in the value of 2. By extension, because 2 + 1 = 3, we can say that 1 and 2 are included in the value of 3. Then, 3 + 1 = 4 which means that 1, 2 and 3 are included in the value of 4 and so on.
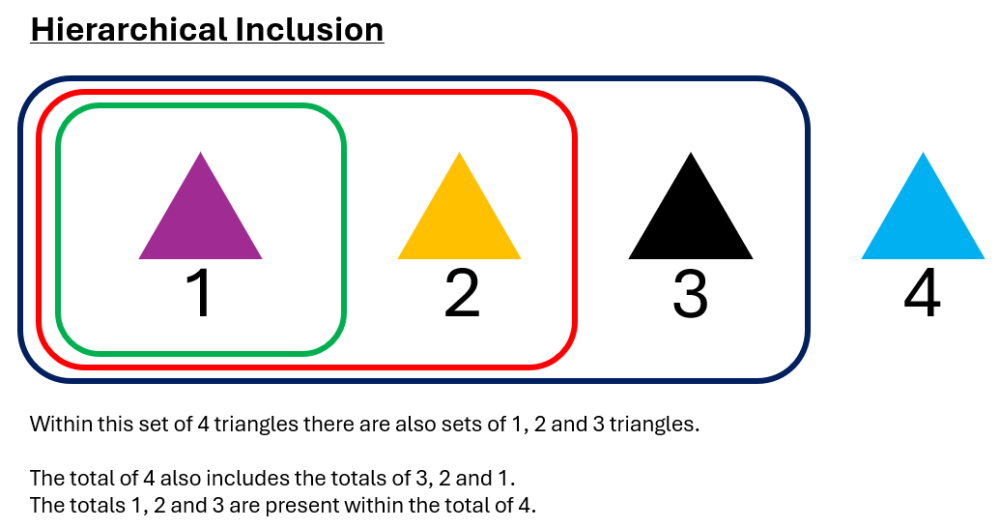
We can use this idea and develop it into a useful maths tool. For example, because 6 + 1 = 7, we can also say that 5 + 2 = 7. We have reduced the 6 by one to leave 5. At the same time, we have compensated the original 1 by adding this 1 to make 2. Thus, we maintain a total of 7 (5 + 2 = 7).
We can do this again, reducing the 5 by one to make 4 and compensating the 2 by adding this one to make 3. A total of 7 is maintained (4 + 3 = 7).
From this idea, we can very quickly develop a set of pairs of numbers that add together to make 7. We call them number bonds to 7. Other bonds, to other numbers, are available.
| Number bonds to 7 | Explanation | ||||
| (7 | + | 0 | = | 7 | starting point. 7 with 0 added is 7) |
| 6 | + | 1 | = | 7 | 7 reduced to 6 (6 is included in 7). 0 compensated to 1. |
| 5 | + | 2 | = | 7 | 6 reduced to 5 (5 is included in 6). 1 compensated to 2. |
| 4 | + | 3 | = | 7 | 5 reduced to 4 (4 is included in 5). 2 compensated to 3. |
| 3 | + | 4 | = | 7 | 4 reduced to 3 (3 is included in 4). 3 compensated to 4. |
| 2 | + | 5 | = | 7 | 3 reduced to 2 (2 is included in 3). 4 compensated to 5. |
| 1 | + | 6 | = | 7 | 2 reduced to 1 (1 is included in 2). 5 compensated to 6. |
| (0 | + | 7 | = | 7 | 1 reduced to 0. 6 compensated to 7) |
We have built up these relationships from the principles of hierarchical inclusion and compensation. The 7 + 0 = 7 and 0 + 7 + 7 relationships are interesting. Both demonstrate a tricky concept. Put simply, if you start with a total and add nothing to it, the total remains the same. The reverse is also true that if you take nothing away from a total, then the total remains the same.

This set of relationships can be put into words by:
If you had zero toy cars and found 7 in the toy box, how many cars would you have to play with?
Or, if you started with 7 toy cars and could find no more more in the toy box, how many would you have to play with?
From Addition to Subtraction with Part-Part-Whole Models
From this additive idea, we can start to develop subtractive ideas too. If we know that 4 + 3 = 7 then 7 – 4 = 3. If we start with a total of 7 and want to know what goes together with 4 to make that 7, then it is 3.
Although expressed as an addition, this is a subtraction:
If we start with 7, and 4 are ‘taken away’ how many do we have left?
Finally, we put this all together as a part-part-whole relationship. This is the idea of 2 parts that, when added together, make the whole. In reverse, when either part is subtracted from the whole we are left with the other part.

Recap – How to Count With Your Child
Let’s recap how to count with your child. The use of concrete representations is vital. This will help them link numbers to the quantities they represent. This one-to-one correspondence lays the foundations of cardinality and number sense.
Then, building on those foundations, we find hierarchical inclusion. This shows that when we count, each new number includes all the numbers we counted before. It’s like adding one more each time.
Finally, using the idea of compensation, we can learn about number bonds and part-part-whole models. This helps your child begin to understand addition and subtraction.
References
WYNN, K 1988. “Psychological foundations of number: numerical competence in human infants.” Trends in Cognitive Sciences 2, 296-303.
TWOMEY FOSNOT, C & DOLK, M 2001. “Young mathematicians at work: constructing number sense, addition, and subtraction.” 31-37.
